[vuoto]
anno 19 numero 37 / 10.24
Biografia
Maria Paola Lombardo è ricercatrice in fisica teorica. Si occupa di particelle elementari e di fisica nucleare delle alte energie, usando principalmente metodi numerici. Attualmente è associata senior presso la sezione INFN di Firenze.
Un salto nel vuoto
Interazioni, temperatura e stabilità
di Maria Paola Lombardo
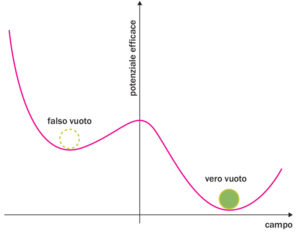
a.
Esempio di curva del potenziale efficace in funzione del valore del campo. Il potenziale nel caso del “falso vuoto” è più elevato rispetto a quello del “vero vuoto”. C’è una specie di barriera tra i due stati. La temperatura, favorendo le fluttuazioni, può aiutare il superamento della barriera e il passaggio verso il “vero vuoto”.
La nostra attuale comprensione del mondo subatomico si basa sull’idea che le particelle elementari siano la manifestazione della fluttuazione di campi quantistici. Una particella di date massa e velocità, esente da interazioni, è l’effetto di un’oscillazione, con una frequenza ben definita, di un opportuno campo. Ciò lascerebbe pensare che lo stato di “vuoto”, cioè di assenza di particelle, debba corrispondere all’assenza di qualunque fluttuazione di campi o, equivalentemente, allo stato in cui tutti i campi sono uniformemente uguali a zero. Invece questo non è possibile, perché anche i campi devono sottostare al principio di indeterminazione di Heisenberg e sono costretti ad agitarsi in un moto incessante, che può essere interpretato come la continua creazione e distruzione di particelle dall’esistenza effimera. Queste fluttuazioni di campi, dette “fluttuazioni del vuoto”, hanno tuttavia un valor medio nullo: possiamo quindi concludere che lo stato di “vuoto” è quello in cui i campi fluttuano intorno allo zero. Questo è lo stato di minima energia per un sistema di particelle non interagenti (vd. Molto rumore per il nulla, ndr).
Quando le particelle hanno interazioni, le corrispondenti fluttuazioni quantistiche non sono più riconducibili solo a oscillazioni di frequenza definita. In questo caso, la loro dinamica (il modo in cui si propagano) si modifica e può essere descritta utilizzando il concetto di “potenziale efficace”. Se, per semplicità, ci limitiamo a considerare un solo tipo di particella, e quindi un solo tipo di campo, il “potenziale efficace” dipende dai possibili valori che quel campo può assumere. Il potenziale può quindi presentare dei massimi e dei minimi, e quelli che qui ci interessano in modo particolare sono proprio i minimi: per avere una rappresentazione figurativa di questo potenziale, si pensi al profilo di una catena montuosa, con vari picchi e valli. Lo stato di minima energia, cioè quello che chiamiamo il “vuoto”, è quello in cui il campo fluttua in fondo alla valle più profonda. La cosa interessante è che il valor medio delle fluttuazioni del campo non è necessariamente uguale a zero, ma dipende da dove si trova la valle più profonda, cioè la posizione (configurazione) del campo in cui il potenziale ha il suo valore minimo.
Il quadro diventa ancora più intrigante se il sistema che vogliamo descrivere con il nostro campo è fatto di particelle interagenti in equilibrio a una certa temperatura. L’effetto della temperatura è quello di modificare il profilo del potenziale efficace e, quindi, in generale, il numero e la posizione delle sue “valli”. Tipicamente, una temperatura alta implica ampie fluttuazioni del campo che inducono “disordine”, facendo sì che il valore medio del campo sia nullo (potenziale efficace con un solo minimo in cui il valore medio del campo è zero), mentre quando la temperatura scende e le fluttuazioni termiche si attenuano può succedere che, per effetto delle interazioni, si manifestino le valli e i picchi del profilo iniziale del potenziale efficace: è come se, mano a mano che la temperatura scende, la vera forma della catena montuosa e delle valli venga poco a poco rivelata. Questa dinamica con profilo di valli e picchi variabile con la temperatura ha interessato (e interessa) il nostro universo, che può essere trattato, con buona approssimazione e su larga scala, come un sistema la cui temperatura scende continuamente mentre esso si espande.
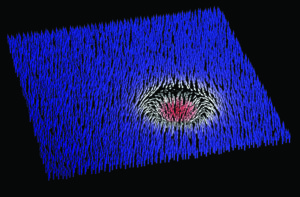
b.
Rappresentazione della prima prova sperimentale di osservazione del decadimento del falso vuoto, ottenuta al Pitaevskii Center for Bose-Einstein Condensation di Trento. Inizialmente gli atomi si trovano in una configurazione in cui sono tutti allineati verso l’alto (il “falso vuoto”). Il decadimento del falso vuoto avviene quando in una porzione limitata di spazio cambia l’orientamento di parecchi atomi e si formano piccole bolle localizzate (le frecce rosse nell’immagine).
Ma cosa succede a un campo che, a una certa temperatura, è soggetto a un potenziale efficace con molte valli? Si posiziona subito in fondo alla valle più profonda? Lo fa uniformemente in tutti i punti dello spazio in cui è definito? Intuitivamente, se il nostro “profilo montuoso” ha una sola profondissima valle, il sistema non avrà esitazioni e sceglierà quella valle. Il vuoto sarà dunque stabile. Può capitare, però, che proprio accanto alla nostra comoda valle si apra, separato solo da una modesta altura, un precipizio rovinoso. Ecco che si delinea un possibile ruolo della temperatura: favorendo le fluttuazioni, la temperatura può incoraggiare il “salto” verso il precipizio, portandoci al di sopra della piccola altura, e poi nel baratro… In questo caso, lo stato di vuoto provvisorio, o “metastabile”, in cui si trovava inizialmente il sistema, lo si chiama “falso vuoto”, mentre il “vero vuoto” corrisponde al minimo più profondo, quello “stabile”. Per un sistema a temperatura decrescente può succedere che la transizione verso il “vero vuoto” avvenga attraverso uno o più stazionamenti provvisori in altri stati di “falso vuoto”. Può anche accadere che regioni diverse dello stesso sistema stazionino per tempi diversi nello stato (o negli stati) di falso vuoto, generando così delle disomogeneità spaziali che possono causare interessanti fenomeni (vd. L’assenza del tutto per il caso dell’universo). È evidentemente molto importante capire quali e quanti “vuoti” siano presenti nei modelli che descrivono i costituenti fondamentali e le loro interazioni e se tra essi ci siano vuoti stabili.
Immaginiamo ora che il nostro potenziale, al diminuire della temperatura, modifichi la forma del suo profilo in modo che si passi da una fase in cui esiste un solo minimo a un’altra in cui quel minimo si separa in due minimi di uguale profondità. Che accade se il nostro profilo montuoso ha due belle valli, della stessa profondità e forma? Per spiegarlo, possiamo usare una citazione di Dante: “intra due cibi, distanti e moventi – d’un modo, prima si morria di fame – che liber uom l’un si recasse ai denti”, che è una delle versioni della storia dell’asino di Buridano. Nel linguaggio del potenziale, si tratta di scegliere tra due vuoti equivalenti, e fatta la scelta, la simmetria si rompe spontaneamente. E di nuovo questo ci porta a parlare di temperatura: la rottura spontanea di simmetria, in cui la simmetria della natura – le due belle valli uguali – non viene realizzata dal nostro sistema, perché spontaneamente ne viene selezionata una, è tipica delle basse temperature. Si parla in questo caso di “transizione di fase”: ad alta temperatura il campo fluttua intorno a un valore medio nullo, a bassa temperatura lo fa intorno a un valore medio diverso da zero. Il valore medio del campo, diverso nelle due fasi, consente di distinguerle – esso si comporta come “parametro d’ordine” del sistema. Il riferimento all’ordine si spiega perché la fase di alta temperatura è tipicamente “disordinata” a causa delle maggiori fluttuazioni termiche. Se il nostro sistema non fosse quello descritto da un campo quantistico fondamentale, ma piuttosto da un insieme di piccole barrette magnetiche disposte su una struttura a reticolo e interagenti tra prime vicine, la fase di alta temperatura sarebbe quella in cui le barrette si orientano disordinatamente lungo le infinite possibili direzioni, producendo una magnetizzazione media uguale a zero, mentre in quella di bassa temperatura si allineerebbero ordinatamente tutte in una sola direzione, producendo una magnetizzazione media diversa da zero. In questo caso il “parametro d’ordine” è la magnetizzazione media.

c.
A sinistra Yoichiru Nambu, a destra Giovanni Jona-Lasinio, i fisici che hanno sviluppato il modello sulla rottura spontanea di simmetria per formazione di condensati, che porta il loro nome.
Un effetto spettacolare della fase di bassa temperatura di sistemi che subiscono transizioni di fase è la formazione di “condensati”, come la “condensazione di Bose-Einstein”, che dà luogo ad esempio alla superconduttività: essa è dovuta alla formazione di coppie di elettroni che condensano formando uno stato superconduttore. In questo caso, il ruolo di parametro d’ordine non è giocato da un campo fondamentale, ma dal prodotto di due campi, ciascuno dei quali è associato a un elettrone. Ma cosa c’entra questo con il vuoto? Ebbene, nel vuoto delle interazioni forti, descritto dalla cromodinamica quantistica (QCD), si forma un condensato di quark e antiquark, e questo condensato è strettamente associato alla rottura spontanea di simmetria di cui parlavamo prima. Esiste un modello molto generale che può descrivere la rottura spontanea di simmetria per formazione di condensati, che è dovuto a Yoichiru Nambu e Giovanni Jona-Lasinio e che viene utilizzato in molti contesti diversi, dalla studio della materia condensata alla meccanica statistica.
C’è un aspetto di straordinaria importanza nello studio delle transizioni di fase: se il sistema passa dalla fase ordinata a quella disordinata in maniera continua, il comportamento del sistema alla transizione dipende solo dalle sue simmetrie e non dal dettaglio delle interazioni microscopiche dei suoi costituenti. Si osserva quindi che sistemi anche molto diversi tra di loro (come, ad esempio, una teoria di campi interagenti a temperatura finita e un sistema di dipoli magnetici) si comportano in modo molto simile vicino alle loro rispettive transizioni di fase. Questa proprietà, nota con il nome di “universalità” e studiata approfonditamente a partire dalla seconda metà del secolo scorso, è considerata un grande successo della fisica teorica.
Biografia
Maria Paola Lombardo è ricercatrice in fisica teorica. Si occupa di particelle elementari e di fisica nucleare delle alte energie, usando principalmente metodi numerici. Attualmente è associata senior presso la sezione INFN di Firenze.


