Un secolo di meraviglia
Dalla prima alla seconda rivoluzione quantistica
di Paola Verrucchi

La meccanica quantistica è una splendida creazione dell’intelletto umano, battezzata purtroppo con un brutto binomio. Il sostantivo “meccanica” è riduttivo; l’aggettivo “quantistica” restringe l’ambito di riferimento. Complessivamente il termine sembra indicare uno strumento dall’uso specifico e limitato. Niente di più lontano da ciò di cui stiamo parlando, ovvero una teoria scientifica di enorme successo per la spiegazione dei fenomeni microscopici conosciuti, che la fisica teorica sta cercando di estendere al mondo macroscopico e ai fenomeni cosmologici e gravitazionali. Sebbene la storia della scienza suggerisca che una descrizione ancora più generale emergerà in futuro, la meraviglia che si prova di fronte a uno strumento tanto elegante e potente è innegabile.

a.
Werner Heisenberg e Niels Bohr, due degli artefici della prima rivoluzione quantistica.
Nei primi decenni del secolo scorso deve essersi trattato di uno spaventato stupore, più che di meraviglia. Stupore per l’estraneità della realtà che la meccanica quantistica descrive rispetto all’esperienza quotidiana, spavento per il potenziale distruttivo nei confronti della fisica classica (forza trainante per illuminismo e rivoluzione industriale e intoccabile in quanto tale).
Il binomio di cui sopra è stato probabilmente funzionale a ridurre tale spavento, nella misura in cui l’aggettivo relega ciò che la teoria descrive a un ambito di cui non facciamo parte, allontanando e rendendo meno spaventose le sue conseguenze. Gli scritti degli scienziati di quel periodo (Max Planck, Albert Einstein, Erwin Schrödinger, Werner Heisenberg, Niels Bohr e tanti altri), e le testimonianze circa le loro appassionate discussioni, mostrano con quanta riluttanza alcuni, o con quanto entusiasmo altri, si ponessero di fronte allo stranissimo mondo che la nuova teoria andava delineando. Ne emerge una conflittualità tipica delle rivoluzioni, ivi incluse quelle scientifiche.
Il confronto con lo sconquasso causato dalla teoria eliocentrica di Copernico, con il sostegno della verifica sperimentale ad essa fornito da Galileo, è pertinente. Doveva certo sembrare assurdo, a una persona che per tutta la vita aveva visto una palla luminosa girare intorno al suo capo, immaginare che quel moto fosse dovuto alla rotazione della terra intorno a se stessa. Nei secoli la cultura occidentale ha accettato questa assurdità, come atto di fede nel metodo scientifico galileiano, ma è stato solo quando siamo andati nello spazio che abbiamo davvero capito cosa significhi essere una minuscola pallina che ruota su se stessa e intorno al suo sole in un immenso universo.

b.
Con i suoi esperimenti sulla disuguaglianza di Bell, il fisico francese Alain Aspect (nella foto) ha contribuito ad avviare la seconda rivoluzione quantistica. Nell’ottobre 2022 è stato insignito del premio Nobel per questi suoi studi.
Torniamo dunque alla meccanica quantistica: i suoi primi cinquant’anni, nei quali collochiamo la cosiddetta “prima rivoluzione quantistica”, sono caratterizzati da una serie ininterrotta di conferme sperimentali tanto straordinarie da far passare in secondo piano la perplessità concettuale che si palesava in alcuni famosi paradossi, come quello del gatto di Schrödinger, e nella formulazione delle prime cosiddette “interpretazioni” della teoria. È il periodo del motto “zitto e calcola”, l’invito a non perdersi nel labirinto delle possibilità offerte dalla meccanica quantistica, limitandosi a usarla come strumento predittivo di grande precisione. Funzionale a questo atteggiamento è la scelta della rassicurante interpretazione “di Copenaghen”, che restringe l’ambito di applicazione della teoria all’infinitamente piccolo, escludendo la possibilità di osservare nella vita di tutti i giorni fenomeni tanto assurdi da mettere in discussione l’oggettività della percezione umana e minare alle fondamenta il castello della fisica classica. Occorre arrivare agli anni ’60 per registrare i primi cedimenti di questa posizione, segnalati in primis dal lavoro del 1964 di John Bell: con tale lavoro il fisico nord-irlandese sfida la comunità scientifica a riportare nei laboratori la discussione sui fondamenti della meccanica quantistica, nel frattempo quasi completamente migrata in ambito filosofico.
La sfida viene raccolta da alcuni fisici visionari come Daniel Freedman, John Clauser e Alain Aspect (gli ultimi due insigniti del premio Nobel della fisica del 2022, assieme ad Anton Zeilinger), solo per citarne alcuni, la cui indagine sperimentale mostrerà che non esistono mondi retti dalle leggi della meccanica quantistica distinti da quelli in cui vige la disciplina della fisica classica: l’universo è quantistico e noi ne siamo parte, anche se la nostra esperienza quotidiana sembra dire il contrario. È la “seconda rivoluzione quantistica”, quella in cui la meccanica quantistica diviene strumento per leggere la realtà che ci circonda e progettare dispositivi da usare e controllare secondo le nostre necessità. E così, a partire dai primi anni ’90 del secolo scorso, diverse tecnologie quantistiche si sviluppano intorno a esigenze di comunicazione, crittografia, computazione e metrologia, mentre la teoria viene ripulita, diventa elegante e si stabilizza su un numero sempre minore di elementi portanti, i cosiddetti “postulati”. E siccome siamo arrivati ai giorni nostri, è opportuno dedicare quel che resta di questo articolo proprio a loro, ai postulati della meccanica quantistica, sorprendenti per la novità della visione e l’eleganza della formulazione.
c.
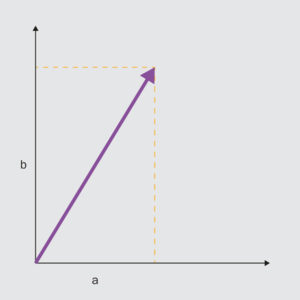
Lo stato di un sistema è descritto da un vettore in un particolare spazio vettoriale, lo “spazio degli stati”. Essendo rappresentati da vettori, gli stati di un sistema possono essere sommati tra loro (“principio di sovrapposizione”): si ottengono in questo modo infiniti altri stati possibili del sistema.
Seguendo un percorso tipico di molte teorie scientifiche, la meccanica quantistica inizia con il dirci come descrivere lo “stato” di un sistema. Stato è un concetto generico, come testimonia l’uso che facciamo del termine quando affermiamo di essere in un pessimo stato o ci chiediamo quale sia lo stato del nostro giardino. Il concetto diventa scientificamente utile quando a esso si associa uno strumento formale in grado di veicolare informazioni sulle proprietà del sistema che in quello stato si trova. In fisica classica tale strumento è il punto in un opportuno spazio: per esempio, in meccanica, un punto nello spazio delle fasi, le cui coordinate rappresentano la posizione e la quantità di moto della particella. Il primo postulato della meccanica quantistica stabilisce invece che lo stato sia formalmente rappresentato da un vettore, detto appunto “vettore di stato”. Dal punto al vettore sembra un passaggio innocuo: i vettori, come i punti, sono oggetti semplici, segmenti orientati introdotti ben prima dell’avvento della meccanica quantistica, abbondantemente usati in fisica classica per descrivere forze, velocità o momenti angolari, o in generale proprietà dei sistemi, e per questo familiari a molti di noi.
Quello che rende il passaggio rivoluzionario, e per certi versi sconcertante, è l’uso del vettore per descrivere lo stato del sistema e non una sua proprietà. Perché sconcertante? Perché una delle caratteristiche principali dei vettori è che possono essere sommati. Molti ricorderanno la regola del parallelogramma. Altri sapranno comunque individuare le componenti orizzontale e verticale di un vettore obliquo, riconoscendo istintivamente che tali componenti si sommano per dare come risultante il vettore stesso. Allo stesso modo una componente di vernice blu si sovrappone a una componente gialla, per formare una vernice verde. L’esempio dei colori ci aiuta a capire che il primo postulato della meccanica quantistica, in breve “lo stato di un sistema è descritto da un vettore”, ci consegna lo sconvolgente “principio di sovrapposizione”, secondo il quale stati diversi di un sistema possono essere sovrapposti, cioè, formalmente, i rispettivi vettori di stato possono essere sommati. Diventa così possibile che un sistema sia contemporaneamente orizzontale e verticale, giallo e blu, 0 e 1 e infine, per assurdo, vivo e morto, come il famoso gatto di Schrödinger.
d.
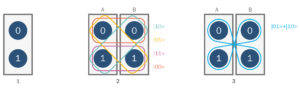
1. Un sistema a due stati (“qubit”) può trovarsi nello stato |0>, nello stato |1> o in una qualunque sovrapposizione di |0> e |1>.
2. Gli stati fattorizzabili di due sistemi A e B a due stati: per esempio, |10> vuol dire che A si trova in |1> e B in |0>.
3. Uno stato “entangled” di due sistemi A e B.
Uno degli aspetti più affascinanti della meccanica quantistica è il modo in cui struttura matematica e descrizione della realtà si corrispondono: il segno “+”, che compare nell’operazione di somma fra vettori, corrisponde precisamente alla congiunzione logica “e” nella descrizione di un mondo in cui i sistemi si possono trovare contemporaneamente in stati diversi. Non si tratta di essere orizzontali o verticali, forse gialli o forse blu, 0 o più probabilmente 1, come si ostinava a sostenere Einstein, il quale non ha mai accettato la sovrapposizione di stati come fenomeno reale (ritenendo fosse un modo sbagliato di giustificare una mancanza di informazione analoga a quella che costringe a un’analisi statistica): la teoria ci dice che un sistema può essere contemporaneamente in più stati diversi. E se questo è già di per sé strano, quando mettiamo insieme due sistemi, le cose si fanno ancora più sorprendenti.
Supponiamo che i due sistemi, che indicheremo con A e B, abbiano ognuno a disposizione due stati, chiamiamoli |0> e |1> per semplicità, usando il simbolo |∙> (ket), introdotto da Paul Dirac: evidentemente la coppia A-B avrà a disposizione quattro stati (|00>, |01>, |10>, |11>), nonché le loro possibili somme, dato il principio di sovrapposizione. A e B potranno essere entrambi 0 e contemporaneamente entrambi 1, cioè nello stato descritto dal vettore |00> + |11>; oppure potranno trovarsi in uno stato in cui, quando A è 0, B è 1, e quando A è 1, B è 0, cioè nello stato descritto dal vettore |01>+|10>. È importante notare che nel ragionamento non c’è riferimento al fatto che A e B siano vicini o lontani, che possano comunicare fra loro oppure no.
e.
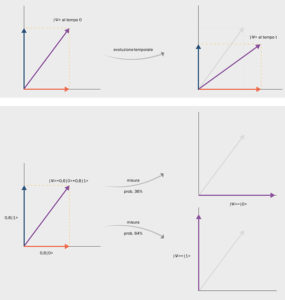
In alto: L’evoluzione temporale di uno stato |ψ>, governata dall’equazione di Schrödinger, è deterministica: dato lo stato iniziale al tempo 0, lo stato del sistema in un qualunque istante successivo è esattamente determinato. In basso: La dinamica della misura non è deterministica. Supponendo che lo stato iniziale del sistema sia una sovrapposizione del tipo |ψ>=0,6|0>+0,8|1>, all’atto della misura il sistema “collassa” istantaneamente, con probabilità (0,6)2=0,36, nello stato |0> e, con probabilità (0,8)2=0,64, nello stato |1> (“regola di Born”). Lo stato in cui si troverà il sistema dopo la misura può essere predetto solo probabilisticamente.
Il loro è uno stato intrinsecamente di coppia: non è possibile dire in che stato sia A senza considerare lo stato di B. In gergo diciamo che lo stato dei due sistemi è “entangled” (un termine inglese che vuol dire “intrecciato”), o anche che A e B sono quantisticamente correlati, con l’avverbio a indicare un legame che resiste, in linea di principio, alla separazione fisica e al passar del tempo. Non si può metabolizzare il principio di sovrapposizione, e l’entanglement che da esso deriva, senza chiedersi cosa succede effettuando una misura su un sistema quantistico, o parte di esso. In altri termini, cosa potrà rispondere un vettore obliquo alla domanda “sei orizzontale o verticale”? O anche: come risponderanno A e B nello stato |00>+|11> alla domanda “siete entrambi zero o entrambi uno”?
Seguendo una logica ferrea, la meccanica quantistica ci insegna che tutte le alternative di risposta che mettiamo a disposizione definendo la nostra domanda sono possibili, e la capacità predittiva della teoria consiste nel fornirci la probabilità con cui otterremo l’una o l’altra risposta. Inoltre, la selezione della specifica risposta avviene contestualmente a un reale cambiamento di stato del sistema: il vettore obliquo, rispondendo “orizzontale”, si sdraierà; A e B, rispondendoci “siamo entrambi 0”, si porteranno nello stato |00>.
L’inevitabile interazione fra noi che domandiamo e il sistema che deve darci una risposta non è trascurabile, come si assume implicitamente in fisica classica, e provoca un cambiamento dello stato del sistema sottoposto a interrogatorio, cioè indagato sperimentalmente.
La descrizione del processo di misura secondo la meccanica quantistica, sintetizzata nel cosiddetto postulato di misura, ci consegna la formula (detta “regola di Born”) per determinare la probabilità di ottenere uno dei possibili risultati (la risposta) facendo una specifica misura (la domanda) a un sistema che si trova in un certo stato, nonché la regola che stabilisce come tale stato cambi in base al risultato ottenuto.

f.
Una figura di diffrazione di elettroni, caratterizzata da una successione di zone più chiare e zone più scure, corrispondenti a un maggiore o minore addensamento di elettroni sullo schermo. Il fatto che gli elettroni producano delle figure di diffrazione è una conseguenza dell’ipotesi quantistica di de Broglie, secondo cui ogni particella si comporta come un’onda.
A volte si racconta questo postulato ammantandolo di stranezza, proponendo come stupefacente il fatto che la misurazione possa modificare lo stato del sistema sperimentalmente osservato. Invece non c’è molto di strano: il trasferimento di informazione implicito nello schema domanda-risposta richiede un’interazione, e questa può sicuramente generare cambiamento negli attori dello scambio.
Certo ci sono ancora molte questioni aperte riguardo a come questo avvenga e perché possa essere ignorato, o quasi, nelle attività di tutti i giorni. Ma questo non dovrebbe inquietare, piuttosto affascinare ed entusiasmare. Affascinare per l’eleganza con cui il linguaggio formale della meccanica quantistica prevede fenomeni assolutamente inattesi eppure reali (cioè sperimentalmente verificati in modo assolutamente indiscutibile). Entusiasmare per le infinite possibilità che tali fenomeni offrono, in applicazioni e nuove tecnologie (come illustrato dagli articoli successivi).
Dedichiamo infine qualche riga a due considerazioni di carattere generale. Allontanandoci temporalmente dal positivismo illuminista, abbiamo imparato che la scienza ha un margine di libera interpretazione. La fisica non fa eccezione, come ci mostra la meccanica quantistica con le sue svariate interpretazioni, tutte accettabili purché compatibili con la rigorosa formulazione e la precisissima capacità predittiva della teoria stessa.
g.
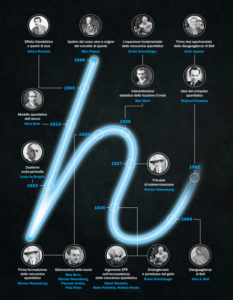
Dalla prima alla seconda rivoluzione quantistica.
A volte la possibilità di essere diversamente interpretata è vista come una debolezza, un presagio di fallimento. Può invece essere considerata una preziosa libertà, della quale riconoscere i ben definiti confini per poi godersela nell’esplorazione del mondo intorno a noi. Peraltro, questa libertà interpretativa deriva da un’altra delle caratteristiche peculiari della meccanica quantistica, ovvero il suo essere costruzione intellettuale profondamente collettiva. Noi parliamo di sistema copernicano, relatività galileiana, meccanica di Newton, elettromagnetismo di Maxwell, gravità di Einstein… ma i padri della meccanica quantistica sono troppi. Anche considerando solo quelli il cui nome compare in una locuzione frequente (costante di Planck, atomo di Bohr, ipotesi di de Broglie, equazione di Schrödinger, regola di Born, principio di indeterminazione di Heisenberg, principio di indistinguibilità di Pauli, equazione di Dirac…), l’elenco è lunghissimo, a testimonianza del fatto che c’è voluto il contributo di molti grandi scienziati per costruire, a partire dagli inattesi e incomprensibili risultati degli esperimenti, una teoria completa e coerente. Ecco, questo è uno dei più importanti insegnamenti che la storia della meccanica quantistica ci consegna: la ricerca scientifica è azione collettiva, condivisione, confronto, discussione e sinergia, forse proprio perché l’universo stesso, che la scienza studia e vuole comprendere, altro non è che uno straordinario esempio di convivenza.










