Entanglement

Entanglement
Al centro del mondo quantistico
di Marco Genovese

a.
Erwin Schrödinger (1887-1961): uno dei padri della meccanica quantistica, è l’autore dell’equazione che descrive l’evoluzione dei sistemi quantistici. Nel 1935 introdusse il concetto di entanglement.

Assieme alla relatività einsteiniana, la meccanica quantistica – la teoria creata per descrivere la fisica “microscopica” (atomi, particelle, ecc.) – è uno dei due pilastri della fisica moderna. Per la maggioranza dei fisici, essa rappresenta la descrizione fondamentale delle leggi della fisica all’interno della quale debbono inquadrarsi tutte le altre descrizioni (ad esempio, la meccanica classica ne sarebbe un limite per i corpi macroscopici).
I sistemi quantistici (cioè le particelle elementari, gli atomi, le molecole, …) sono descritti in termini di poche proprietà osservabili (posizione, energia, quantità di moto, spin, polarizzazione, …) che ne definiscono lo “stato”. Tali sistemi possono essere composti da più sottosistemi, ad esempio gli elettroni e il nucleo in un atomo, o due fotoni emessi assieme.
L’entanglement (termine inglese che potremmo tradurre con “intreccio”, ma che è ormai entrato anche nel linguaggio scientifico italiano) è una proprietà peculiare dei sistemi quantistici (definita da Schrödinger il “tratto” peculiare della meccanica quantistica), che lega indissolubilmente parti diverse di uno stato quantistico inducendo correlazioni tra i risultati delle misure effettuate su sottosistemi. Queste correlazioni non possono essere descritte come proprietà preesistenti, ma emergono solo al momento della misura e sono indipendenti dalla distanza tra i sottosistemi. Il fenomeno dell’entanglement, dal 1935, quando venne introdotto, è fonte di un acceso dibattito sul suo significato e sul suo impatto sui fondamenti della meccanica quantistica.
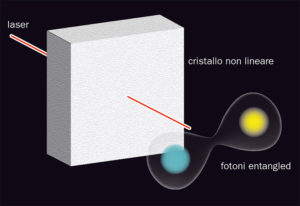
Cerchiamo dunque di capire un po’ più in dettaglio in che cosa consiste. Immaginiamo di avere una sorgente che emette due fotoni (le “particelle” quantistiche fondamentali di cui la luce è costituita). I fotoni sono caratterizzati dalla loro energia e, essendo quanti di luce, cioè pacchetti di onde elettromagnetiche, dal piano di vibrazione del campo elettrico, la cosiddetta “polarizzazione” (quella che viene selezionata dagli occhiali 3D dei cinema, permettendoci di vedere figure leggermente diverse dai due occhi e quindi un’immagine tridimensionale).

In alcuni fenomeni si producono due fotoni con polarizzazione non definita, ma comunque opposta. Ovvero, se un fotone ha polarizzazione orizzontale (H, dall’inglese horizontal), l’altro deve averla verticale (V) o viceversa (vd. fig. b). Per tale stato la polarizzazione del singolo fotone non è determinata prima della misura. Supponiamo ora che i due fotoni siano inviati uno a un osservatore sulla Terra (Alice), l’altro a uno, ad esempio, su Marte (Bob). Appena Alice misura la polarizzazione del suo fotone, immediatamente fissa quella del fotone di Bob: se Alice trova H (nel 50% dei casi), Bob ha V e viceversa. (Si noti che la meccanica quantistica non può predire il risultato della misura, ma solo la probabilità del risultato). Tale risultato è indipendente da come si orientano i polarizzatori. Ad esempio, se Alice e Bob li orientano a 45 gradi rispetto agli assi orizzontale/verticale, ottengono sempre polarizzazioni opposte. Quindi, in questo fenomeno (detto “EPR” dalle iniziali di Einstein, Podolsky e Rosen che lo introdussero in un loro celebre lavoro del 1935), una misura compiuta da Alice determina in maniera immediata anche il valore che otterrà Bob sul suo fotone, relativamente a una osservabile (in questo caso la polarizzazione), il cui valore in meccanica quantistica non è fissato prima della misura.

b.
I fotoni entangled possono essere generati inviando della luce laser su particolari cristalli, in cui i fotoni del laser si convertono in coppie di fotoni di frequenza minore (“fluorescenza parametrica”).

La domanda che ci si può porre (e che Einstein si pose!) è se in realtà questi risultati non siano predeterminati da qualche variabile nascosta, ovvero se la meccanica quantistica non sia una teoria incompleta. In tal caso il fatto che la meccanica quantistica non possa predire i risultati, ma solo le probabilità di ottenerli, deriverebbe dal fatto che ignoriamo queste variabili aggiuntive. Sarebbe come avere due palline, una blu e una rossa, e due scatole. Qualcuno, a nostra insaputa, mette la pallina rossa in una scatola, la blu nell’altra. Poiché noi ignoriamo dove le abbia messe, possiamo solo supporre che al 50% la pallina blu sarà nella scatola 1 e la rossa nella 2 o viceversa. Però le palline sono sin dall’inizio in una scatola o nell’altra (la variabile nascosta). L’attribuire una probabilità alla misura dipende dal fatto che ignoriamo questa variabile. Potrebbe essere lo stesso per i due fotoni (e più in generale per tutti gli stati entangled)? Sorprendentemente la risposta è no! Nel 1964 John Bell dimostrò che nessuna teoria a variabili nascoste in cui non si possa trasmettere un segnale immediatamente a distanza arbitraria (cioè una teoria “locale”) può riprodurre tutte le correlazioni che si possono osservare tra stati entangled. Questa scoperta aprì la strada a un confronto sperimentale tra la meccanica, nella sua versione standard, e sue possibili “estensioni” basate su variabili nascoste locali. Una serie di esperimenti sempre più perfezionati, ultimati nel 2015, ha dimostrato inequivocabilmente che le correlazioni osservate tra due fotoni entangled sono quelle previste dalla meccanica quantistica. Questo risultato è davvero eccezionale. Non si esclude solamente una possibile alternativa alla meccanica quantistica, ma un’intera classe di teorie: ovvero qualsiasi teoria in cui le correlazioni dovute all’entanglement siano prodotte da variabili nascoste in maniera locale.

c.
John Bell (1928-1990): nel 1964 dimostrò che nessuna teoria, in cui i valori delle osservabili siano descritti da variabili nascoste locali, può riprodurre tutti i risultati della meccanica quantistica. In particolare, non può riprodurre le correlazioni previste per gli stati entangled (“disuguaglianze di Bell”).

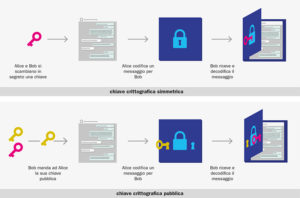
d.
Due metodi di comunicazione crittografica. Il primo si basa sulla condivisione di una sequenza casuale di bit: la chiave. Se questa è perfettamente casuale, lunga quanto il messaggio (in bit) e usata una sola volta, per un teorema matematico il messaggio criptato non può essere decodificato in alcun modo. Il secondo metodo si basa sulla difficoltà computazionale di invertire alcune funzioni. Il metodo è più semplice in quanto non richiede di condividere chiavi arbitrariamente lunghe. La sua sicurezza però non è garantita: un computer quantistico potrebbe comprometterne la sicurezza (vd. anche in Fotoni e segreti, ndr).