Sulle tracce felpate del gatto di Schrödinger

Sulle tracce felpate del gatto di Schrödinger
Alla ricerca di eventuali limiti della teoria quantistica
di Catalina Curceanu

a.
Illustrazione del paradosso del gatto di Schrödinger.

La meccanica quantistica è la teoria di maggiore successo di sempre. Essa viene utilizzata all’interno dei computer e dei telefonini, sta alla base del modello standard della fisica delle particelle elementari o di una TAC in ospedale. Tuttavia, malgrado siano trascorsi più di 100 anni da quando è emersa come un pilastro della conoscenza del mondo e malgrado i suoi innumerevoli successi, è anche la teoria che ci fa discutere più di tutte. Ci interroghiamo ancora sui suoi significati, sulle sue (apparentemente) strane proprietà e anche sui possibili limiti di validità della teoria stessa che, va detto subito, non abbiamo ancora sfiorato. Tuttavia, termini quali entanglement oppure sovrapposizione di stati, proprietà quantistiche per eccellenza, riconducibili alla funzione d’onda che descrive il comportamento dei sistemi quantistici, sono entrati a far parte del bagaglio culturale di molti di noi. Non solo, le stesse proprietà vengono sempre di più utilizzate nelle nuove tecnologie quantistiche: dai computer e sensori quantistici alla crittografia quantistica (vd. Comunicare nell'era dei quanti, ndr).
Tra gli aspetti più dibattuti della fisica quantistica c’è il cosiddetto “problema della misura”: come fa la funzione d’onda, che si trova in una sovrapposizione di stati, a collassare in uno di questi stati quando viene misurata? Questo problema è anche all’origine del cosiddetto paradosso del gatto di Schrödinger.

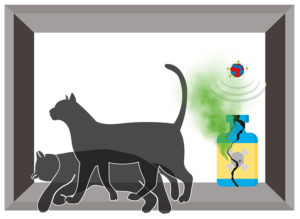
Per far capire ai suoi colleghi quanto fosse strana la meccanica quantistica applicata a un sistema macroscopico, Erwin Schrödinger inventò in un articolo del 1935 il famoso esperimento mentale che ha come protagonista un gatto chiuso in una scatola assieme a una sostanza radioattiva, che rappresenta il sistema quantistico. La sostanza radioattiva si trova in una sovrapposizione di stati, con una probabilità del 50% che emetta (o non emetta) radiazione dopo un tempo di (diciamo) 10 minuti. Se la radiazione viene emessa si aziona un meccanismo che rompe una fiala contenente del veleno, con conseguente morte dello sfortunato gatto. Ma, poiché lo stato è determinato dalla misura, trascorsi i 10 minuti, prima di aprire la scatola, lo stato non è ancora determinato (l’apertura della scatola corrisponde alla misura). E quindi, in quel momento, coerentemente con il fatto che la sostanza si trova in una sovrapposizione di stati, la risposta alla domanda: “che fine ha fatto il gatto?” è che il gatto è sia vivo che morto. Il gatto di Schrödinger è diventato il paradigma del problema della misura e dopo tutti questi anni la comunità scientifica sta ancora discutendo su quale potrebbe essere la soluzione del paradosso. Non che non ci siano proposte: anzi, ce ne sono sin troppe! Alcune di esse assumono che in natura esistano soltanto particelle che avrebbero delle traiettorie determinate da condizioni aggiuntive (nel passato si parlava di onde che guidavano le particelle): si tratta dell’interpretazione di de Broglie-Bohm. C’è poi l’affascinante interpretazione dei “molti mondi”, dovuta a Hugh Everett III: ogni volta che viene eseguita una misura il mondo si divide, e ogni mondo realizza una delle possibilità. In questa interpretazione c’è dunque un mondo in cui il gatto è vivo e un altro in cui il gatto è morto. Queste due tipologie di interpretazioni, benché affascinanti, offrono – almeno per ora – poco appiglio ai fisici sperimentali: non c’è modo di confermare una delle due, in quanto le previsioni sperimentali sono identiche, in linea di massima, a quelle della meccanica quantistica standard. C’è però un’altra soluzione: una modifica radicale della meccanica quantistica, attraverso quelli che vengono definiti i “modelli di collasso dinamico”.

b.
Rivelatore Broad Energy Germanium Detector al laboratorio di bassa radioattività dei Laboratori Nazionali del Gran Sasso dell’INFN.

I modelli di collasso risolvono il problema della misura all’origine, modificando l’equazione di Schrödinger, con l’aggiunta di termini non lineari e stocastici. I nuovi termini devono essere però aggiunti con criterio: non si possono contraddire le evidenze confermate della meccanica quantistica. Da una parte bisogna preservare proprietà quantistiche ben note delle particelle, quali l’interferenza dei fotoni oppure degli elettroni, una manifestazione implicita della sovrapposizione di stati, dall’altra i termini in più devono provocare il collasso della funzione d’onda evitando la sovrapposizione di stati negli oggetti macroscopici: le sedie, i pianeti, le stelle e noi stessi dobbiamo essere ben localizzati, e non stare “sia qua che là”, in una sovrapposizione di stati. Il collasso deve essere dunque amplificato dal numero di particelle contenute nell’oggetto: per poche particelle il collasso deve avvenire in un tempo lunghissimo, mentre per un oggetto macroscopico, composto di un numero enorme di particelle, deve essere praticamente istantaneo. Esistono vari modelli di collasso – da quelli introdotti sin dagli anni ’60 da Frigyes Karolyhazy e sviluppati ulteriormente da GianCarlo Ghirardi, Alberto Rimini, Tullio Weber, Philip Pearle e Angelo Bassi, a quelli nei quali il collasso è collegato alla gravità – i cosiddetti modelli di Diòsi-Penrose.

c.
Raffreddamento del moto di una nanosfera di vetro allo stato fondamentale per mezzo di una cavità ottica nell’esperimento viennese di Markus Arndt.